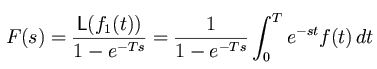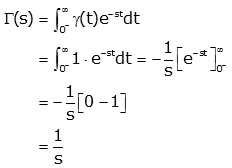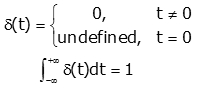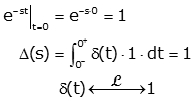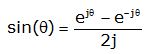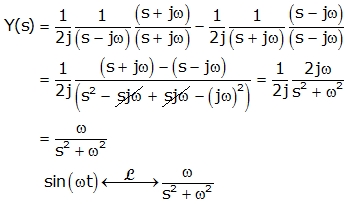Next part of Nasir’s tutorial…Enjoy!
Introduction
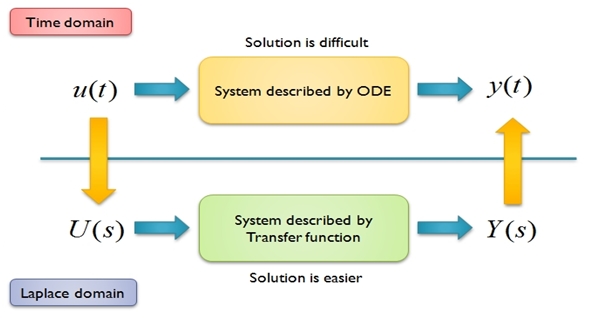
In the previous two parts of the tutorial we discussed the Laplace integral and how it is used to solve differential equations. Let’s recall Laplace integral over a function f (t):
Then we discussed Region of Convergence (ROC) of Laplace transform. The convergence or divergence of output depends solely on the values of s. So the set of values of s that converge the output signal lie in a region branded as ROC.
Since it has already been conferred that Laplace Transform converts integral and differential equations into simple algebraic equations. Let’s study the Laplace integral for some elementary function and analyze the outputs.
Definition
A function is said to be periodic if it repeats the same values after a particular interval or period. There are many phenomena like oscillation and wave etc. that demonstrate periodicity. Mathematically, a function is periodic if:
f(t+T)=f(t)
Where, T is any constant and is greater than zero. For every value of t the condition written above must satisfy. T is known as the period.
Geometrically a function is called periodic if its graph displays translational symmetry. Most common examples of periodic functions are the trigonometric functions like sine, cosine etc. They have a period of 2 radians. Another good example of the periodic functions is triangular wave. It is defined by:
f(t+2)=f(t)
For any value of t, we can demonstrate Laplace transform of almost all periodic functions with help of a proposition which we will discuss later in this article. A function that doesn’t repeat its values over a certain period of time is called aperiodic.
Proposition
We have proposition to calculate Laplace transform of periodic functions. It says that, if f is a periodic function which has a period T and f_1 is one period of the function then, we can write the Laplace transform of the function as:
Laplace Transform of Some Important Elementary Functions
To transform a periodic function using Laplace transform we need to transform their domain from time to Laplace domain. We need to evaluate the integral in order to find the Laplace transform. Let’s have a look at some important elementary functions’ Laplace transform.
The Unit Step Function:
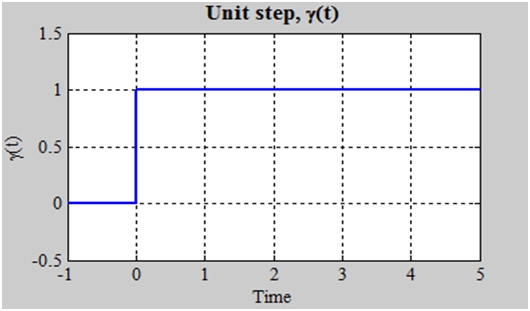
We know that unit step function is written as:
Graphically it is represented as:
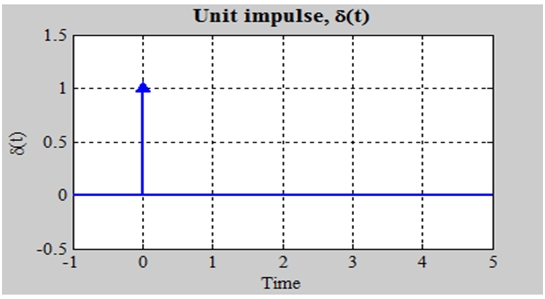
In some cases, the definition of step is changed so that the inequality of bottom becomes strict inequality (t>0) which leaves ɣ (0) undefined. Also there is discontinuity at t=0 but we have drawn a vertical line to make understanding easy and to show that the blue line is single function.
Now, we will find the Laplace transform by applying the definition.
Thus,
The Unit Impulse Function:
To give you brief idea what is impulse function, it is basically everywhere but at t=0, where this is infinity large. The impulse function area is one. It can be represented on graph by an arrow whose height is equal to its area.
Now, we will find Laplace transform by applying:
We will use impulse property that is impulse is 0 everywhere but at t=0, the upper limit of integral will be 0+
As we know that e-st is continuous at t=0, so we can say it is constant from t=0– to t=0+. Now we can put value of e-st evaluated at t=0.
By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.
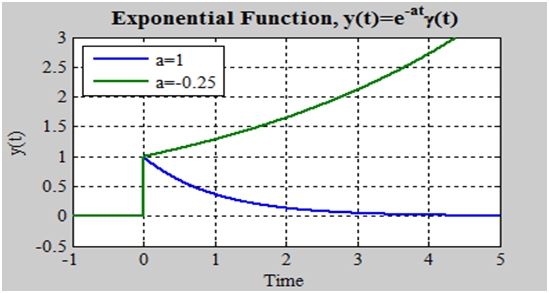
The Exponential Function:
We are considering exponential for t>0.
It is considered as exponential if the function is 0 for t>0. We can define that function in pieces as seen in first definition or can define as exponential multiplied b unit step as seen in second definition. The second ne is more efficient, so we usually take that one. As all the functions for t>0 is zero, by multiplying with γ (t) will not show exact γ (t) and will regularly be implicit.
If a<0 the function falls to zero but if a>0 then function increases freely. Mostly we studyfalling to zero exponential and they are generally in the systems.
To find Laplace transform we will apply:
As we know that for all positive t γ (t) is one, so we can scrap it from integral.
You can see that γ (t) is implicit in last equation. If a=1 we get a step function and L(s) =1/s
The Sine Function:
Like earlier, we will use definition to find Laplace transform:
We can take Euler’s identity for sine:
Thus,
As we have done this integral in above exponential function
Taking common denominator
Laplace Transform of Some Other Elementary Functions
It’s over for today, see you next time!
Nasir.