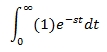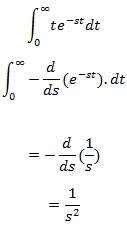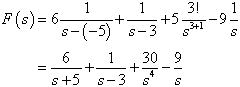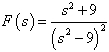Our very productive member Nasir decided to write another series of tutorials. This time, he wants to focus on Laplace Transform, which is all about mathematics. Are you ready?
Introduction
The purpose of Laplace transformation is to solve different differential equations. There are a number of methods to solve homogeneous and non-homogeneous equations but Laplace and Fourier transform are used widely. Laplace transform comes in to use when we have to solve the equations that cannot be solved by any of the previous methods invented.
In this tutorial we will be introducing you to Laplace transform, its basic equation and how it can be used to solve various algebraic problems. Laplace transform is more expedient when it comes to non-homogeneous equations. It is one of the easiest methods to solve complicated non-homogeneous equations.
Definition
The Laplace transform converts integral and differential equations into algebraic equations. Although it is a different and beneficial alternative of variations of parameters and undetermined coefficients, the transform is most advantageous for input terms that piecewise, periodic or pulsive.
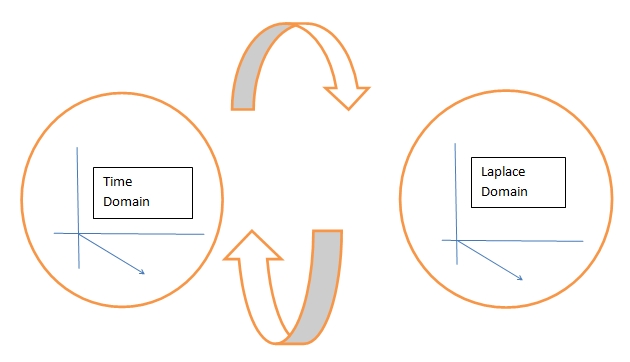
In simple words, Laplace transform converts time domain signal into frequency domain, which is depicted more clearly in below figure:
For a function f (t) with boundary conditions, 0 ≤ t < ∞, Laplace integral is written as:
The above transform is denoted by L (f (t)). This shows that the integrations is taken over t. The upper and lower boundary conditions of t are applied when we solve the equation where, e-st is the integrator here. In a simple way we can write it as:
L (f (t)) = F(s)
The transform is a function of variable s.
Laplace Integral
The part 
, which is in frequency domain, is known as Laplace integral for the function f (t), which is in time domain. It is has defined limits and depends on the value of variable son.
Few important cases are discussed below, which are usually used while applying Laplace on any function. These cases are derived using basic mathematics.
- Case 1
If we put f (t) =1, the Laplace integral becomes:
After integrating, (1/s).e-st will be obtained along with the boundaries. After applying boundaries it becomes, 1/s.
- Case 2
If we put f (t) =t, the Laplace integral becomes: - Case 3
If we put f (t) =t² then the Laplace integral is written as:
From case 2 we know that:
So,
If we observe the above results we might conclude that,
And
Examples
In examples, we will find Laplace transforms of the functions:
We will transform individual functions and will put constant in function to get the result.
.
Now,
We can have,
Uses of Laplace Transformation in Control System
Laplace transform is useful mathematical tool to explain the integrals in the interval from 0 to infinity. It is also used for analyzing and designing the analog signals.
Also we know that control systems chiefly deals with analog systems. So usually it is obligatory to take integral from 0 to infinity unless initial conditions are not provided. Laplace transform converts into frequency domain from function which makes evaluation easy.
We can get the time response of the given system by taking inverse Laplace transform that is ratio of Laplace of output to the Laplace of input.
Conclusion
In this tutorial we have introduced you to Laplace transformation along with Laplace integral. It basically shows how we can commute simple algebraic equation from integral equations.
We have also discussed some example to make Laplace transformation easier to understand. Laplace transform is useful instrument in control system as we have pointed out above.
In next article we will discuss about ROC of Laplace transform which will be helpful in understanding Laplace transform.
Nasir.