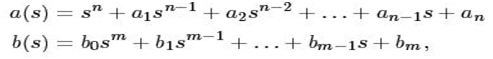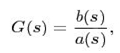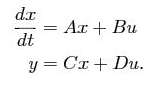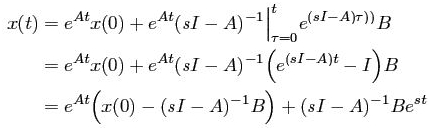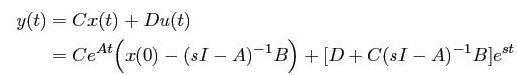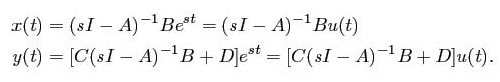What is Transfer Function?

[admin]

Last but one tutorial from the series about the Control Systems topic written by Nasir, our active member of the community. Will this definition help you?

Introduction

In Analyzing and designing of any system, the most important factor is the mathematical modeling of that system. There are many mathematical models to describe control systems.

In physics, transfer function maybe defined as mathematical representation (in terms of frequency) of interrelation between input and output in linear time uninterrupted systems with zero pint equilibrium and zero initial conditions. If talking particularly about control systems then it can be defined as the ratio of the Laplace transform of the output variable to the Laplace transform of the input variable, with all zero initial conditions.

Transfer function is function of complex variables. The transfer function can be obtained by simple algebraic jugglery of differential equations that illustrates the system. Transfer function can represent higher order systems also, even infinite dimensionless systems which regulates on partial differential equations.

Transfer Function

The input-output explanation of system is elementally the spreadsheet of all possible input-output pairs. Like for linear system, spreadsheet can be described by single input single output pair. For example the impulse response or the step response.

Transfer Function of a Linear System

Consider the linear input-output system, the differential equation (1) that express it will be:

Where, u is the input and y is the output the differential equation is completely described by two polynomials:

The characteristic polynomial of system is polynomial a(s). Taking u (t) = e^st as input to find transfer function so the output will also be an exponential function that will be y (t) = y₀ e^st. Inserting signals in equation (1), we get:

If a , it will give,

The transfer function of this linear system thus will be rational function,

Note that, a(s) and b(s) are given above as polynomial of system.

Transfer Function of Exponential Signals

In linear systems, exponential signals plays vital role as they come into sight in solving differential equation (1). It also comes in picture when we see impulse response of a linear system.

Exponentials or sum of exponentials can signify many signals. A constant signal is e^αt with =0. We can show this signal in explicit form as:

As mentioned above, combination of exponentials can represent many signals as it’s a combination of cosine as well as sine function so let’s examine a linear system which is answering back to the exponential input signal u(t) = e^st we consider the state space system:

Think the input signal as u (t) = e^st, suppose that where is the ith eigenvalue of A. The state is as follows:

The integral can be solved since

The result of the above equation can now be written as:

This is a linear combination of exponential functions with exponents e^st and

In which are eigenvalues of A.

Only one term of the output is proportional to the input that is: u (t) = e^st. This is the pure exponential response when the initial state is:

x (0) = (sI-A)^-1B

Both state and output are proportional to input and output only has exponential response.

The ratio of output and input is the transfer function of the system and is written as:

The response of a system to an exponential input can be written as:

Conclusion

As we move towards the end of this control tutorial we have a now almost a complete insight of all the entities in a control system. In this article we have discussed transfer function which is input-output explanation of system. We studied transfer function of linear systems.

In the next tutorial that will be the last one we will study poles and zeros of a control system and the major differences between them. I hope you will stay tuned to us as this will be the last article of this chain.

Nasir.

[Anonymous]

Genuinely no matter if someone doesn’t be aware of after that its
up to other viewers that they will help, so here it happens.

[Anonymous]

I got this website from my buddy who shared with
me about this web page and now this time I am
browsing this web page and reading very informative articles here.

[Author]

Posts