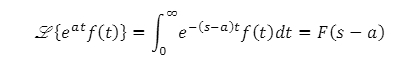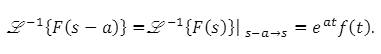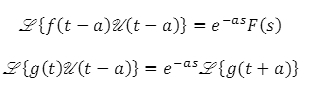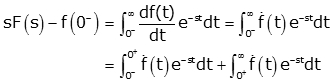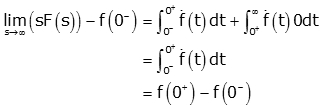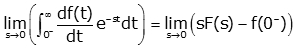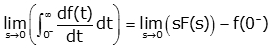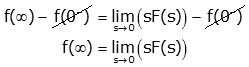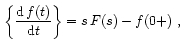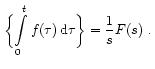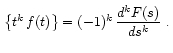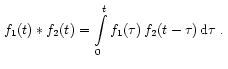Theorems of Laplace Transform

[admin]

Our loyal member Nasir continues his article series about Laplace Transform. Today, let him sum up some theorems…

Introduction

Laplace transform is a way of transforming differential equations into algebraic equations. The Laplace integral is given by:

As we studied Laplace transform of some basic elementary functions and properties of Laplace transform, there are a few theorems that do apply on Laplace transform and make them easier to solve.

We will also see how we can use those theorems over Laplace integral just like we did with the properties. Some of the Laplace theorems are also considered as properties so you may feel like you have studied them already in the properties article but here we shall discuss the a slightly different context.

Let’s have a look at the basic theorems:

1. Existence Theorem

The foremost theorem analysis whether or not Laplace transform of a function exists. It says that for a piecewise continuous function f (t), L (f (t)) exists if and only if t ≥ 0 and s > t.

2. The First Shifting Theorem

The first shifting theorem states that, if a function f(t) is in time domain and get multiplied by e^-at, the result of s-domain shifts by amount a.

Mathematically,

3. Second Shifting Theorem

The second shifting theorem has quite similarities with the first one but the outcomes are entirely different. The unit step function converts exponential function from t-domain in s-domain. Mathematically the theorem can be stated as:

4. First Translation theorem

This theorem is applicable when a function say, f (t) is multiplied by an exponentiale^at. The Laplace transform of their product is given as:

When we evaluate this integral we get the first translation theorem. So we have:

Here we have replaced s by s-a in F(s).

Inverse Form of the First Translation Theorem

Since we know that,

The inverse of the theorem is given as:

Since this is inversed form so, here we have replace s-a by s.

5. Second Translation Theorem

Consider a function f (t-a) and a unit step function u (t-a), the transform of their product is given as e^-asF(s). Similarly for another function g (t) and the same unit step function u (t-a), the transform of their product is given as e^-asL {g (t+a)}.

Mathematically, second translation theorem is represented as:

Inverse Form of the Second Translation Theorem

To find the inverse of second translation theorem, take the inverse of above equation:

6. Initial Value Theorem

This theorem we also discussed in properties. The theorem for initial value is

Or

To prove this theorem, we will take derivative rule:

We then evoke the Laplace transform definition and breakup integral in two parts

Taking limit s going to infinity

On left hand side, the second term doesn’t depend on s and can be pulled out. On the right hand side, the first term can be pulled out giving same justification. Also if infinity is to be put for s in second term then the exponential term goes to zero.

f (0-) is canceled from both sides and only initial value theorem remains.

7. Final Value theorem

You may remember that we discussed this theorem in properties. Unlike initial value theorem, in final value theorem only final value of function remains

Or

The limitation of this theorem is that it can be used only when final value if it exists, like for functions cosine, sine and ramp function there is no final values. To show the final value theorem, we will start with Laplace transform derivative

Taking limit s goes to zero,

For s→0, the exponential term dies out from the integral. In addition we can pull out f (0-) from limit as it is not dependent on s.

We can calculate integral

In the left hand expression, there is no term which depends on s so we can take off limit. By simplifying we will get final value theorem

8. Superposition theorem

If we take a₁ and a₂ as constants then theorem will be

9. Complex Shifting Theorem

Taking a>0 as an arbitrary constant

10. Similarity Theorem

For an arbitrary constant a>0

11. Derivative theorem

Taking f(t) as casual function of time, for which the derivative exists if t>0

12. Integral theorem

Function’s integral is represented by

13. Complex differentiation theorem

By this theorem, it is explained that a differentiation of a function F(s) in time domain corresponds to a multiplication with time t.

14. Convolution in the time domain

If taking two functions f₁ (t)and f₂ (t) which is represented by symbolization f₁ (t) * f₂ (t), the theorem will be

Convolution of two functions gives the multiplication of those functions, that is

That’s all about the theorems of Laplace Transform. In the coming articles, we are going to discuss the inverse Laplace Transform which has its own importance in determining the stability of any function.

Nasir.

[Author]

Posts