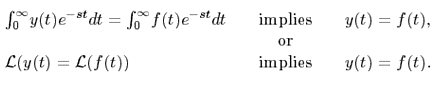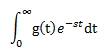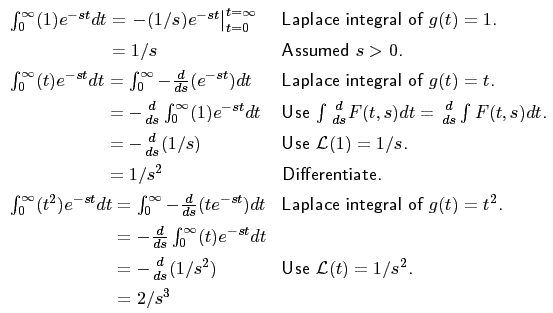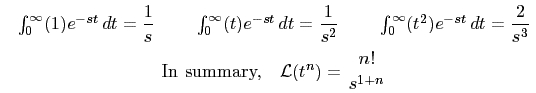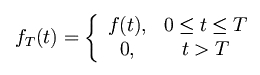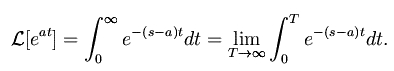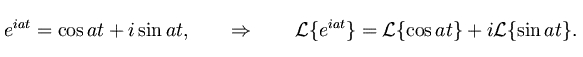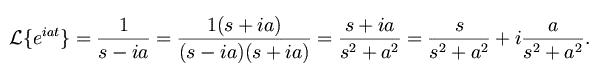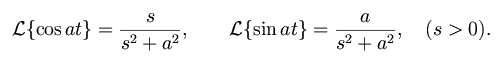Introduction to Laplace Transform

[admin]

Check the next part of Nasir’s tutorial on Control Systems. What do you know about Laplace Transform?

Definition

Laplace transformation converts differential and integral equations into rather simple algebraic equations. Laplace transform is nothing but a simple operational tool, used to solve linear differential equations with constant coefficients.

The transformation is only applied to general signals and not to sinusoidal signals. Also, it cannot handle steady state conditions. It enables us to study complicated control systems with integrators, differentiators and gains.

On basis of Laplace transformation we analyze LCCODE’s and circuits with several sources, inductors, resistors and capacitors.

For a given function f (t) such that t 0, its Laplace transformation is written as F(s) = L {f (t)} and is written as:

From the above equation we conclude that the transformation converges when the limit exists and diverge when it does not. The L notation recognizes that integration always proceeds over t = 0 to t=1 and that the integral involves an integrator dt instead of the usual dt.

Laplace transformation method

Laplace transformation reduces the problem of solving a differential equation to an algebraic problem. Laplace theory is based on Lerch’s cancellation law which is given as follows:

In a differential equation, y(t) is an unknown variable depending on time.

Laplace Integral

The Laplace integral of a function g (t) is given as:

The integral formulae are derived by illustrating g (t) = 1, g (t) = t and g (t) = t²

By summarizing we get:

Some important transformation rules:

Following are some properties of general calculus that can be implemented on the transformation:

• The sum of two integrals can be combined:



• Lerch’s cancellation law is applied on Laplace transformation:



• Integration by parts or sometimes called the t-derivative rule:



• Constant can be written out of the integral:

Laplace Transforms of Periodic Functions

At times the non-homogenous term in a linear differential equation is a periodic function. Any function f (t) can be said a t-periodic function if we write it as f (t+T) = f (t) like the period of sine and cosine is radians where period of tangent is

For a t-period the function is written as:

Provided that t 0

Now the Laplace transform is given as:

• Example 1:



Using the definition we have:



For improper integral to converge we need s > a. Here:



• Example 2:

Let’s have a look at Laplace transform of Sin at and Cos at.

Using the Euler’s formula we can write:



By Laplace transform we have:



By comparing real and imaginary parts we get:

Conclusion

Though the topic of Laplace transform is much wider, we have tried to enclose the basics of it in this article. What is the basic idea and concept of Laplace transform and how it works. We discussed a couple of examples to elaborate it more.

As we move on to the end of these tutorials we will study the most important part in the upcoming one that is Transfer Function. It is the factor on which a control systems depends so stay tuned to us for the tutorial.

Nasir.

[Author]

Posts