Diode Characteristics

[admin]

Last time our devoted member Nasir introduced you to semi conductors, now let him tell you about the characteristics of the diode, an important component.

Diodes are the basic types of power semiconductor switching devices. In this article we are going to discuss some of the basic characteristics of diodes and their properties. It is a two terminal device with one terminal marked as positive and the other one as negative.

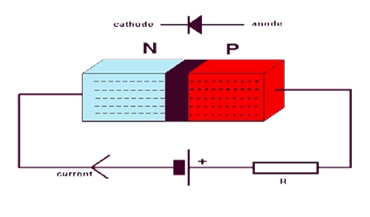
If we talk with respect to the semiconductor properties of the diodes, the two terminals are the terminals of the pn-junction. The p region is known as the anode electrode and the n region is known as the cathode electrode.

Power Diode acting as a Switch

Now the question that arises is that how does a diode acts as a switch. It is a one way device, which only allows the flow of electricity in one direction only. When the anode i.e the p terminal of the pn junction is at a higher potential than the cathode, the flow of current occurs from positive to negative as per convention.

We connect the positive terminal of the diode to the positive terminal of the battery and the negative terminal of the diode to the negative terminal of the battery. Hence the diode acts as a closed switch allowing current to flow through it in one direction. The current cannot flow back in the opposite direction from the negative terminal to the positive one. In this state the diode is known to be Forward Biased.

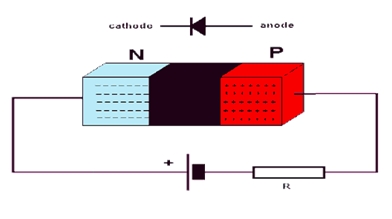
Now when the anode is at a lower potential than the cathode, the current cannot flow from positive to negative since the potential of positive is lower than the negative. The positive terminal of the diode is connected to the negative terminal of the battery and the negative terminal to the positive one of the battery. In this state the diode acts as an open switch, blocking the flow of current through it and is known to be Reverse biased.

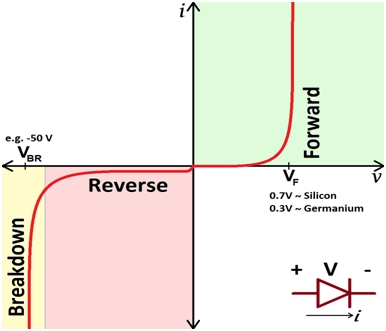
This is the literal behavior we tend to consider for an ideal diode, that it lets the flow in one direction and no current in the other direction. But unfortunately things are not ideal in this world. In case of a real practical diode, there is a very small amount of reverse or leakage current as well, which flows but is almost negligible. This can be represented as follows:

When the potential of the cathode increases such that the voltage across the diode is negative and big in magnitude, the width of the depletion region increases and the junction breaks down since the diode is unable to control the reverse flow of current and is known to be in the Breakdown region.

In short, the semiconductor power diode acts as a switch by allowing the flow of current in one direction and switching it on and off according to the potential applied at its terminals. Due to their diverse properties they are being used in many industries and applications nowadays.

We will consider their different types and applications in the next tutorials since now you are familiar with the basic operation of a semiconductor power diode and its function as a switching device.

Nasir.

[Author]

Posts