Cost efficient W.A.G.E.S management: energy meter is key !
(Water Air Gas Electricity Steam)
From my point of view, I think that Energy management is a major action in all Energy Efficiency programs.
If you can’t measure it, you can’t manage it!
The first thing to do if we want to optimize the consumption of a building is to know, ie to measure and record in a database, all the consumptions for making analysis and having a clear vision on the division of consumptions in the building.
When I say all the consumptions, I think not only electrical power but also the consumption of water, gas, fuel, heat and cold energies.
Therefore, it will be possible to
- Assess real building energy performance, while Energy Performance Certificates rely on theoretical calculations
- Identify and evaluate opportunities for energy savings
- Evaluate energy saving investments real profitability
- Identify drifts, abnormal consumptions and maintain the best energy performances by acting on
– the occupants behaviour
– the energy saving system settings
– the leakages, bad uses; etc…
However, a solution with such capabilities must have an installation cost that can be amortized in a few years. It should be also very easy to implement.
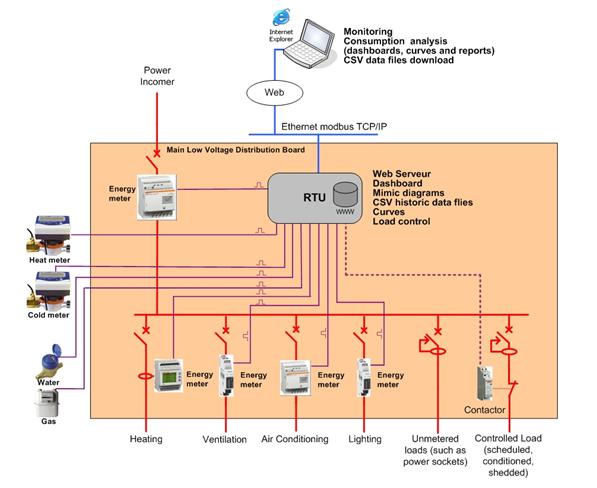
We don’t need to measure the consumption of highly sophisticated equipment. Energy Meter delivering pulses is very cheap and with pulses, we can measure all the energy streams. For example, we can use the little EN40 power meter for single phase feeder up to 40A.
The example given below is for small & medium size building such as a school, hotel, office building, shopping centre …
We must have now a RTU (Remote Terminal Unit), which could be a web server, that can generates easily the
- CSV files for each metering channel: the Remote Terminal Unit calculates and stores
– 10 or 15′ power demand and consumption
– Hour, day, week, month and year average consumption datas (difference of the pulse totalizer data between the period) - Dashboards
- Mimics diagrams
- Curves
- Reports
The RTU, remote terminal unit, could also have the possibility to drive an output for load shedding.
On user initiative, it is possible to connect to the RTU web server to see
- dashbords
- mimic diagrams
- data files and curves
- download CSV data files for Excel analysis
- order the output
This solution could involve all types of buildings in my opinion. Even at home, I see the good, because actually I am unable to know the details of my consumption, whether my consumption is in an acceptable average or not and identify priorities for actions.
What do you thinks about a simple and cheap installation like this allowing you to have a fully understanding of all energy streams?
Do you know some solutions like this in the market?
Emmanuel Bernier
great post, many thanks
DO YOU HAVE ANY ELECTRICAL WIRING ABOUT POWER MANAGEMENT SYSTEM
What’s the brandname and type of the RTU?
The RTU must have several features like:
1. for the hardware
• a big memory capacity for storage all the data during several months (for 10’/15’, hours and day average consumption data) and several years (for week, month and year average consumption data)
• digital inputs used for counting pulses or read status of circuit breakers or acquire tariff periods
• digital outputs for load shedding to act on reduction of energy consumption
• analog inputs if we want to analyse consumption with output information like temperature.
2. for the configuration
A simple configuration tool to set-up the installation easily. The main functionalities of this tool are:
• enter a name for each measurement channel
• enter energy type (water, gas, heat, …)
• enter weight of one pulse
• choose several recording periods (10’, 15’, 1h,1w,1m…)
• generate dashboards, reports and mimics diagrams
3. for the software
• must be a web server
• can generate CSV files of values from the database 10’ or 15’, hour, day, week, month and year records consumption
• can generate curves for analyses
• offer the possibility to download CSV data files for Excel analysis.
I know currently a RTU called iRIO or RIO that has these features and I am interested to know if there are other devices of this type in the market.
what is the procedure for getting the admission & fees strucure for energy management
I use a Power Meter myself, and it is really helpful because it allows me to see how much energy my appliances use so I can reduce my energy bill.