New article by an electrical engineer from Venezuela. Thank you to all the experts who participate in this community! Enjoy and don’t forget to leave a comment if you want to share your thoughts on the electrical contactor.
Nowadays, there is an increasing need for users to take control of the comfort and safety systems installed in their area (air conditioner, lightning, and others) [1]. There are powerful reasons for this, the main one is the birth of a new trend, that goes back to the year 1999 [2], known as Building Automation Systems (BAS). This is related to the need of having control over systems by adding a special panelboard, like a PLC, a relay, a control panel, among others.
There is a second reason, and could be pretty obvious for some: energy is expensive and users cannot afford to waste this valuable resource, so, they need to control it.
When it comes about electrical installations, the most basic methods of control are the switches (more commonly used for lighting circuits) and the electrical contactor for a wider range of applications.
The first ones are made for local control, this means, somebody has to be present to activate the mechanism and perform an action. On the other hand, the latter one is used when the control is performed remotely, that is when commands are executed from an automatic system distant from the circuit they supervise.

Fig1: A common contactor | picture: Electrodepot on Amazon
The contactor is constituted of a set of power contacts, a set of auxiliary contacts, a coil, a mechanism that stores the energy necessary to change the state of the contacts (commonly a spring) and an envelope, the surface of the device.
The coil is connected to the circuit that generates the control signal, that is, where the push buttons, the PLC, and any device that triggers a command are located. When the coil is energized by the control signal according to the manufacturer ratings, the whole set of contacts change their state.
The power contacts (also called poles) work directly on the live circuit that has installed the array of devices to be controlled. They cannot perform a fault clearance, rather an overload condition, however, they are used the most to just open or close a circuit in a normal state. These contacts can be either make (normally open) or type break (normally closed).
The auxiliary contacts are used to trigger an action on a different circuit, typically to activate an alarm when the coil is activated or deactivated. These contacts have different features to the main contact ones. They normally cannot withstand the operating conditions and their main purpose is to allow reckon of their new condition in the control system. They can also be either make or break types.
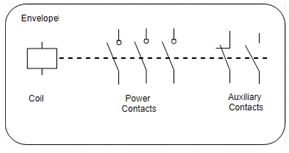
Fig2: Electrical representation of a contactor
Electrical contactor: best reasons for using it in your BAS design
There are other electrical devices that can be used to perform remote control of an electrical circuit like relays. But, the reason for using contactors in an automated system is that they are designed for heavy duty, if they are under the correct maintenance cycle (according to manufacturer instructions and working cycle), their performance will be good enough for your needs in a BAS design, especially when you are working with circuits that will be switching frequently and managing a considerable current magnitude.
Another reason for using them is that they can be easily repaired. Their mechanism is simple, so it is easy to use spare parts to solve the problem, thus saving you from an indisposed circuit control for a long period of time.
Related to the statement above, let me mention some scenarios that I came across.
First scenario: You wish to control a large lighting system of an industrial installation
In such scenario, the first thing you should do is to ask where you should put the control mechanism.
The first option will be as near as possible of the load center of that particular circuit. Meaning that a high current is passing through those cables and could be meaningful having installed a strong device that handles such a circuit.
The next thing to do is to observe if there are noise, vibrations, or movements affecting the circuit somehow. These will confirm that a contactor will be the right choice for this environment.
Second scenario: You wish to control a set of loads under certain circumstances
I remember a time when I had to deal with an uncommon situation in which, there was a backup generator for an industrial plant, whose loads were exceeding the ratings of the generator by far. Therefore, it was not possible to keep the generator active unless those loads decreased.
Since the company did not want to spend money installing an emergency load center for the main loads (should be maintained in service at all cost), I managed to get a solution for them (after talking with a manufacturer) dropping loads instantly when a control signal is received using contactors with break power contacts.
Thus, when, activated, the contacts open, dropping non-important loads, leaving only the main ones still in services.
Electrical contactor: final thoughts
The electrical contactors should come into the scene when you need to take control (on-off) of the energy supplied by a specific circuit since they manage line currents, the best way to use them is near the source, that is, the load center.
Since their coil also manages line voltages, you can use a signal control right from a circuit nearby, thus, saving you the need of another component (a common transformer to reduce line voltage to standard 12-24 V, the case of relays).
They need maintenance, but this is a good feature since most of their parts can be replaced with new ones, unless of course, the device is damaged.
References

You actually make it seem so easy along with your presentation however I in finding this topic to be actually something that I believe I would by no means understand.
It sort of feels too complex and extremely vast for me. I’m
having a look ahead to your subsequent publish, I will try to get the hold of it!
thank you.
nice article