In the previous article, Nasir discussed transfer function of control system. Now check the last but one article of his tutorial: Difference between Poles and Zeros of a Control System…
Introduction
The input-output explanation of system is elementally the spreadsheet of all possible input-output pairs. Like for linear system, spreadsheet can be described by single input single output pair, e.g. the impulse response or the step response.
Transfer function is function of complex variables. The transfer function can be obtained by simple algebraic jugglery of differential equations that illustrates the system. Transfer function can represent higher order systems also, even infinite dimensionless systems which regulates on partial differential equations.
The frequencies for which the values of denominator and nominator become zero in a transfer function are called Poles and Zeros. Poles and Zeros analyze the performance of a system and check the stability. The values of Poles and Zeros control the working of a system. Usually the numbers of Poles and Zeros are equal in a system and in some cases number of Poles is greater.
Definition of Poles
Poles are the roots of the denominator of a transfer function. Let us take a simple transfer function as an example:
Here Poles are the roots of D(s) and can be evaluated by taking D(s) = 0 and is solved for s. Generally, the number of Poles is equal or greater than Zeros. When s approached a pole the value of denominator becomes Zero making the value of transfer function reach infinity.
To determine the response, a system the location of Poles is analyze along with the values of real and imaginary parts of each pole. Real part determines the exponential and imaginary part determines sinusoidal values.
Definition of Zeros
Similar to Poles, Zeros are the roots of nominator of a transfer function. For same above transfer function Zeros can be determined by taking N(s) = 0 and solving for s. The number of Zeros is lesser or equal to the Poles. Zeros mean that the output at those frequencies is zero.
Differences between Poles and Zeros of a transfer function
Let us have a look at the differences between Poles and Zeros and their effects for a given function:
1. Definition:
-
-
- Poles are the roots of the denominator of a transfer function.
- Zeros are the roots of the nominator of a transfer function.
-
2. Determination:
-
-
- Poles are determined by equating D(s) with 0 and solving for s. Zeros are determined by equating N(s) with 0 and solving for s.
-
3. Amount:
-
-
- The number of poles is always greater or equal to the Zeros.
- The numbers of Zeros are lesser or equal to Poles.
-
4. Determination of output:
-
-
- Poles in a transfer function explain that the output has reached to infinity.
- Whereas, the zeros in a transfer function indicate that the output has reached to zero.
-
5.Effect of Additional Poles and Zeros In first order systems:
-
-
- Additional Poles delay the response of a system.
- Left half-plane zeros speed up the response of a system and the right half-plane cause the response to go in the opposite direction.
-
6. Effect of Additional Poles and Zeros in Second order systems:
-
- Additional Poles in a dominantly second order system decrease the number of oscillations.
- Additional Zeros in a dominantly second order system increases the number of oscillations.
Conclusion
The frequencies that turn nominator or denominator zero are called zero and poles of a transfer function respectively. They determine the stability and working of a system.
Here, I have summed up the series of tutorials regarding control systems. I have tried to study various aspects of control systems. I hope that the chain of articles was useful for you and you gave gained some insight about control systems.
Nasir.
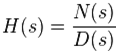
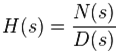
Thank you so much for this post! One of the most useful articles on the internet!!